3. Interpretación geométrica de la derivada
Manipula la siguiente animación. Coloca el punto a donde quieras y haz que h se acerque a cero.
Fíjate que la recta que en principio une los puntos A y B es secante a la curva pero a medida que estos puntos se acercan, la recta se va convirtiendo en tangente a la curva.
Importante
Si tenemos una función f(x), la derivada de la función en x=a, f '(a), es la pendiente de la recta tangente a f(x) en el punto de abscisa x=a .
De esta forma, si tenemos una función f(x) , su función derivada f '(x) es la función que en cada punto toma el valor de la pendiente de la recta tangente a f(x) en ese punto.
El siguiente vídeo te explica gráficamente este hecho:
De este hecho, podemos sacar la ecuación de la recta tangente y normal o perpendicular a una curva en un punto, usando la ecuación punto-pendiente de la recta; la pendiente es f '(a) y el punto por el que pasa la recta (a, f(a)):
Ecuación recta tangente en x = a: 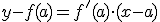
Ecuación recta normal en x = a: 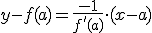
Ejemplo
Recta tangente a la función f(x) = tg(x) en x=0
Curiosidad
La derivada, como hemos dicho es la pendiente de la recta tangente, y si recuerdas de cursos anteriores, la pendiente de una recta, además de indicarnos el crecimiento y decrecimeinto de la recta, nos daba el ángulo de inclinación de dicha recta respecto al eje OX, pues dicha pendiente, era el valor de la tangente del ángulo que formaban la recta y eje OX.
Por tanto, la derivada de la función en x=a, f '(a) es también el valor de la tangente del ángulo que forma la recta tangente a la función en x=a y el eje OX.